904. 水果成篮

你正在探访一家农场，农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示，其中 fruits[i] 是第 i 棵树上的水果 种类 。

你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：

• 你只有 两个 篮子，并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
• 你可以选择任意一棵树开始采摘，你必须从 每棵 树（包括开始采摘的树）上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到下一棵树，并继续采摘。
• 一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。

给你一个整数数组 fruits ，返回你可以收集的水果的 最大 数目。

思路

一个滑动窗口的问题，要求窗口内最多有两种不同的元素，然后找到最大的窗口长度。

class Solution 
{
public:
    int totalFruit(vector<int>& fruits) 
    {
        int n=fruits.size();
        unordered_map<int, int>cnt;//键值对，键表示水果类型，值表示该类型水果数量

        int left=0,ans=0;
        for(int right=0;right<n;right++)
        {
            cnt[fruits[right]]++;
            while(cnt.size()>2)
            {
                int out=fruits[left];
                cnt[out]--;
                if(cnt[out]==0)
                {
                    cnt.erase(out); //当某类水果（例如类型 out）在窗口内的数量减少到 0 时，将其从哈希表中彻底删除。
                }
                left++;
            }
        ans = max(ans,right-left+1);
        }
        return ans;
    }
};

1. right（右指针）
   • 功能：表示当前窗口的右边界，负责扩展窗口（向右移动）。
   • 行为：遍历数组，每次将 fruits[right] 加入窗口，并更新哈希表 cnt 中对应水果类型的计数。
   • 目标：探索可能的更优解（更大的窗口）。
2. left（左指针）
   • 功能：表示当前窗口的左边界，负责收缩窗口（向右移动）。
   • 行为：当窗口内水果种类超过 2 种时，从哈希表中减少 fruits[left] 的计数。如果计数归零，则从哈希表中删除该类型。
   • 目标：确保窗口始终满足条件（最多两种水果类型）。

哈希表的优势

• 键值对存储：键（int）表示水果类型，值（int）表示该类型的数量。

思考

个人觉得在滑动窗口时条件判断十分重要，为了达到动态变更数组长度，while循环十分重要，if仅能变动一次则跳出，不符合要求。

76. 最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

class Solution {
    // 判断当前窗口 cnt_s 是否完全覆盖目标 cnt_t
    bool is_covered(int cnt_s[], int cnt_t[]) {
        // 遍历所有大写字母（ASCII 范围 'A'-'Z'）
        for (int i = 'A'; i <= 'Z'; i++) {
            // 若当前字符在窗口中的数量不足，返回 false
            if (cnt_s[i] < cnt_t[i]) return false;
        }
        // 遍历所有小写字母（ASCII 范围 'a'-'z'）
        for (int i = 'a'; i <= 'z'; i++) {
            if (cnt_s[i] < cnt_t[i]) return false;
        }
        return true; // 所有字符数量均满足要求
    }

public:
    string minWindow(string s, string t) {
        int m = s.length();
        // ans_left 初始化为 -1，表示尚未找到有效窗口；ans_right 初始化为 m（最大可能值）
        int ans_left = -1, ans_right = m; 
        int cnt_s[128]{}; // 记录窗口内字符出现次数（ASCII 共 128 个字符）
        int cnt_t[128]{}; // 记录目标 t 的字符出现次数
        
        // 统计目标字符串 t 中各字符的出现次数
        for (char c : t) {
            cnt_t[c]++; // c 的 ASCII 码作为索引，直接更新对应位置计数
        }

        int left = 0; // 滑动窗口左指针
        for (int right = 0; right < m; right++) { // 右指针逐步扩展窗口
            cnt_s[s[right]]++; // 将右指针字符加入窗口计数
            
            // 当窗口满足覆盖条件时，尝试收缩左边界以找到最小窗口
            while (is_covered(cnt_s, cnt_t)) {
                // 若当前窗口更小，更新答案记录
                if (right - left < ans_right - ans_left) {
                    ans_left = left;  // 记录窗口左端点
                    ans_right = right; // 记录窗口右端点
                }
                cnt_s[s[left]]--; // 左指针字符移出窗口，计数减少
                left++;           // 左指针右移，缩小窗口
            }
        }
        
        // 若未找到有效窗口（ans_left 仍为 -1），返回空字符串，否则截取子串
        return ans_left < 0 ? 
            "" : 
            s.substr(ans_left, ans_right - ans_left + 1); // 子串长度 = 右-左+1
    }
};

s.substr 的作用是什么？

• 函数定义：s.substr(pos, length) 返回字符串 s 中从位置 pos 开始、长度为 length 的子串。

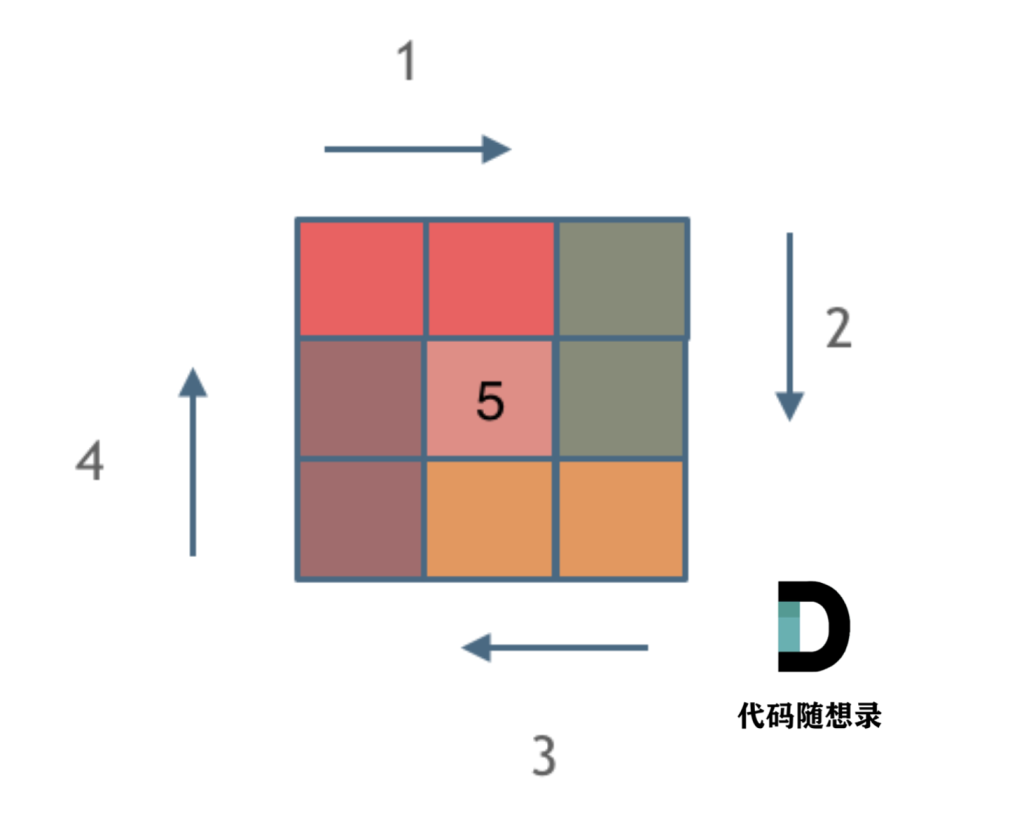
59. 螺旋矩阵Ⅱ

给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

思路

模拟顺时针画矩阵的过程:

• 填充上行从左到右
• 填充右列从上到下
• 填充下行从右到左
• 填充左列从下到上

class Solution 
{
public:
    vector<vector<int>> generateMatrix(int n) 
    {
        vector<vector<int>> res(n,vector<int>(n,0));//使用vector定义一个二维数组，n×n维用0填充的数组。
        int startx=0,starty=0;
        int loop=n/2;
        int mid=n/2;
        int count =1;
        int offset=1;
        int i,j;
        while(loop--) //先条件判断，再自减
        {
            i=startx;
            j=starty;
            //四个for循环模拟转了一圈
            for(j;j<n-offset;j++)
            {
                res[i][j]=count++;
            }
            for(i;i<n-offset;i++)
            {
                res[i][j]=count++;
            }
            for(;j>starty;j--)
            {
                res[i][j]=count++;
            }
            for(;i>startx;i--)
            {
                res[i][j]=count++;
            }
            startx++;
            starty++;
            offset+=1;
        }
        if(n%2)
        {
            res[mid][mid]=count;
        }
        return res;
    }
};

54. 螺旋矩阵（看不懂）

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

class Solution 
{
public:
    vector<vector<int>> generateMatrix(int n) 
    {
        vector<vector<int>> res(n,vector<int>(n,0));//使用vector定义一个二维数组，n×n维用0填充的数组。
        int startx=0,starty=0;
        int loop=n/2;
        int mid=n/2;
        int count =1;
        int offset=1;
        int i,j;
        while(loop--) //先条件判断，再自减
        {
            i=startx;
            j=starty;
            //四个for循环模拟转了一圈
            for(j;j<n-offset;j++)
            {
                res[i][j]=count++;
            }
            for(i;i<n-offset;i++)
            {
                res[i][j]=count++;
            }
            for(;j>starty;j--)
            {
                res[i][j]=count++;
            }
            for(;i>startx;i--)
            {
                res[i][j]=count++;
            }
            startx++;
            starty++;
            offset+=1;
        }
        if(n%2)
        {
            res[mid][mid]=count;
        }
        return res;
    }
};

LCR 146. 螺旋遍历二维数组（看不懂）

给定一个二维数组 array，请返回「螺旋遍历」该数组的结果。

螺旋遍历：从左上角开始，按照 向右、向下、向左、向上 的顺序 依次 提取元素，然后再进入内部一层重复相同的步骤，直到提取完所有元素。

class Solution {
public:
    vector<int> spiralArray(vector<vector<int>>& array)
    {
        if (array.empty()) return {};
        int l = 0, r = array[0].size() - 1, t = 0, b = array.size() - 1;
        vector<int> res;
        while(true)
        {
            for (int i = l; i <= r; i++) res.push_back(array[t][i]); // left to right
            if (++t > b) break;
            for (int i = t; i <= b; i++) res.push_back(array[i][r]); // top to bottom
            if (l > --r) break;
            for (int i = r; i >= l; i--) res.push_back(array[b][i]); // right to left
            if (t > --b) break;
            for (int i = b; i >= t; i--) res.push_back(array[i][l]); // bottom to top
            if (++l > r) break;
        }
        return res;
    }
};