35. 搜索插入位置

题目：给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

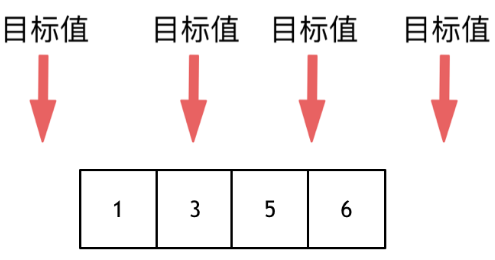
• 目标值在数组所有元素之前
• 目标值等于数组中某一个元素
• 目标值插入数组中的位置
• 目标值在数组所有元素之后

class Solution 
{
public:
    int searchInsert(vector<int>& nums, int target) 
    {
        for(int i=0;i<nums.size();i++)
        {
            if(nums[i]>=target)
                return i;
        }
    return nums.size();
    }
};

假设无重复元素

① 左闭右闭区间：

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0;
        int right = n - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle;
            }
        }
        // 分别处理如下四种情况
        // 目标值在数组所有元素之前  [0, -1]
        // 目标值等于数组中某一个元素  return middle;
        // 目标值插入数组中的位置 [left, right]，return  right + 1
        // 目标值在数组所有元素之后的情况 [left, right]， 因为是右闭区间，所以 return right + 1
        return right + 1;
    }
};

② 左闭右开区间：

class Solution 
{
public:
    int searchInsert(vector<int>& nums, int target) 
    {
        int n=nums.size();
        int left=0;
        int right=n;
        while(left<right)
        {
            int middle=left+((right-left)>>1);
            if(nums[middle]>target)
                right=middle;
            else if(nums[middle]<target)
                left=middle+1;
            else return middle;
        }
        return right;
    }
};

总结

确定要查找的区间到底是左闭右开[left, right)，还是左闭又闭[left, right]，这就是不变量。

然后在二分查找的循环中，坚持循环不变量的原则。

34. 在排序数组中查找元素的第一个和最后一个位置

题目：给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

寻找target在数组里的左右边界，有如下三种情况：

• 情况一：target 在数组范围的右边或者左边，例如数组{3, 4, 5}，target为2或者数组{3, 4, 5},target为6，此时应该返回{-1, -1}
• 情况二：target 在数组范围中，且数组中不存在target，例如数组{3,6,7},target为5，此时应该返回{-1, -1}
• 情况三：target 在数组范围中，且数组中存在target，例如数组{3,6,7},target为6，此时应该返回{1, 1}

寻找右边界

确定好：计算出来的右边界是不包含target的右边界，左边界同理。

// 二分查找，寻找target的右边界（不包括target）
// 如果rightBorder为没有被赋值（即target在数组范围的左边，例如数组[3,3]，target为2），为了处理情况一
int getRightBorder(vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
    int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
    while (left <= right) { // 当left==right，区间[left, right]依然有效
        int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
        if (nums[middle] > target) {
            right = middle - 1; // target 在左区间，所以[left, middle - 1]
        } else { // 当nums[middle] == target的时候，更新left，这样才能得到target的右边界
            left = middle + 1;
            rightBorder = left;
        }
    }
    return rightBorder;
}

寻找左边界

// 二分查找，寻找target的左边界leftBorder（不包括target）
// 如果leftBorder没有被赋值（即target在数组范围的右边，例如数组[3,3],target为4），为了处理情况一
int getLeftBorder(vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
    int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
    while (left <= right) {
        int middle = left + ((right - left) / 2);
        if (nums[middle] >= target) { // 寻找左边界，就要在nums[middle] == target的时候更新right
            right = middle - 1;
            leftBorder = right;
        } else {
            left = middle + 1;
        }
    }
    return leftBorder;
}

处理三种情况

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int leftBorder=getLeftBorder(nums,target);
        int rightBorder=getRightBorder(nums,target);
        if(leftBorder==-2 || rightBorder==-2) return {-1,-1};
        if((rightBorder-leftBorder)>1) return {leftBorder+1,rightBorder-1};
        return {-1,-1};
    }
private:
    int getRightBorder(vector<int>& nums,int target){
        int n=nums.size();
        int left=0;
        int right=n-1;
        int rightBorder=-2;
        while(left<=right){
            int middle=left+(right-left)/2;
            if(nums[middle]<=target){
                left=middle+1;
                rightBorder=left;
            }
            else
                right=middle-1;
        }
        return rightBorder;
    }
    int getLeftBorder(vector<int>& nums,int target){
        int n=nums.size();
        int left=0;
        int right=n-1;
        int leftBorder=-2;
        while(left<=right){
            int middle=left+(right-left)/2;
            if(nums[middle]>=target){
                right=middle-1;
                leftBorder=right;
            }
            else
                left=middle+1;
        }
        return leftBorder;
    }
};